** VERSION 0.9.9.386R CHANGELOG **

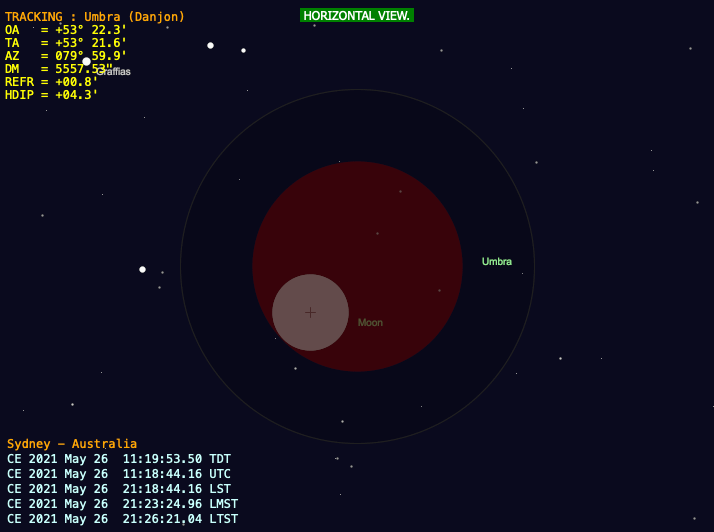
(1) – Let’s talk about Lunar Eclipses. I decided to revert back to Danjon’s rules for computing Lunar Umbra and Penumbra diameters and take into account of the displacement from the Center of Figure (COF) of the Moon with respect to the Center of Mass (COM), provided by the ephemeris. This allowed me to compare my result with F. Espenak predictions (those published on EclipseWise, the most recent I suppose) obtaining coincident results. By the way, Espenak proposes an even more rigorous system that takes into account the ellipticity of the shape of the earth’s shadow and the variation of position angle, the Herald-Sinnott method, promising even better results. His post about that is an interesting reading indeed and can be found here. The original paper by Herald and Sinnot can be found here.

---

(2) – The possibility to have a rigorous search for penumbral, umbral and totality contacts is now given by a new terminal window, T5, where in analytical form, it is explained which values must be achieved for each type of contact. Basically it is the same logic that must be applied to the distance panel already present for the other objects. In order to reach a better graphical fit I added into the Preferences Window a flag showing the Geocentric Moon Radius instead of Topocentric. This flag should be used only during a Lunar Eclipse analysis, then it must be turned off.

---

(3) – After computing Lunar Standstills, now minimum and maximum of the year are shown.

Generated by Uruk_One v.0.9.9.377R
 Topocentric Lunar Standstills computed for the year : 2021
 Location Name : Paris - France
 Longitude     : +  2° 19' 48.000"
 Latitude      : + 48° 52' 12.00"
 DEC and RA at True Equinox of Date.
 Iterative computing by means of DE440/DE441.

 2459226.06934   CE 2021 Jan 11  13:39.8 UTC   -25.232°   269.568°
 2459226.95406   CE 2021 Jan 12  10:53.8 UTC   -25.805°   284.029°
 2459227.81586   CE 2021 Jan 13  07:34.8 UTC   -24.884°   297.885°
 2459240.49503   CE 2021 Jan 25  23:52.8 UTC   +24.188°   092.506°
 2459241.40128   CE 2021 Jan 26  21:37.8 UTC   +24.464°   105.724°
...........................................
...........................................
...........................................
...........................................
 2459567.64225   CE 2021 Dec 19  03:24.8 UTC   +25.171°   086.022°
 2459568.53878   CE 2021 Dec 20  00:55.8 UTC   +25.941°   098.321°
 2459569.44989   CE 2021 Dec 20  22:47.8 UTC   +25.544°   110.917°

 Minimum Standstill : CE 2021 Nov 08  15:26.8 UTC  DC = -27.296°
 Maximum Standstill : CE 2021 Nov 23  02:06.8 UTC  DC = +25.981°
 
End computing

---

(4) – Greatly improved the precision of Lunar Phases computing for distant epochs. The header of the result window should be self explanatory.

---

(5) – Final improvement to the 30 millennia Canon of Solar and Lunar Eclipses. My number crunching server running Linux has computed again all the events with a resolution of ±1s. This should be now the maximum error of the TDT time indicating the Greatest of Eclipse.

---

(6) – ASTEROIDS – The new code related to Asteroids is under test. I implemented what’s necessary for downloading via CURL astorb.dat but download times were indecent (minutes, wtf) so decided to say so long to Lowell Observatory (and thanks for all the fish, of course) and use the IAU Minor Planets Center file, MPCORB.DAT, which only takes a few seconds to be picked up.

---

(7) – Changed the behaviour of PAR(tiality) and TOT(ality) leds. Now when TOT is on, PAR is turned off.

---

(8) – Terminal 6 is active but temporarily shows only test values I will need later for a graphical representation of total/annular solar eclipses. Values refer to Besselian Elements, Gamma, and the geographical coordinates of the place lying on the Central Line computed at the date shown on the top.

---